ICLR 2023: TimesNet 论文阅读笔记
Introduction
这篇文章主要提出了一个泛化的时间序列模型,主要聚集在时序变化建模。
作者观察到:
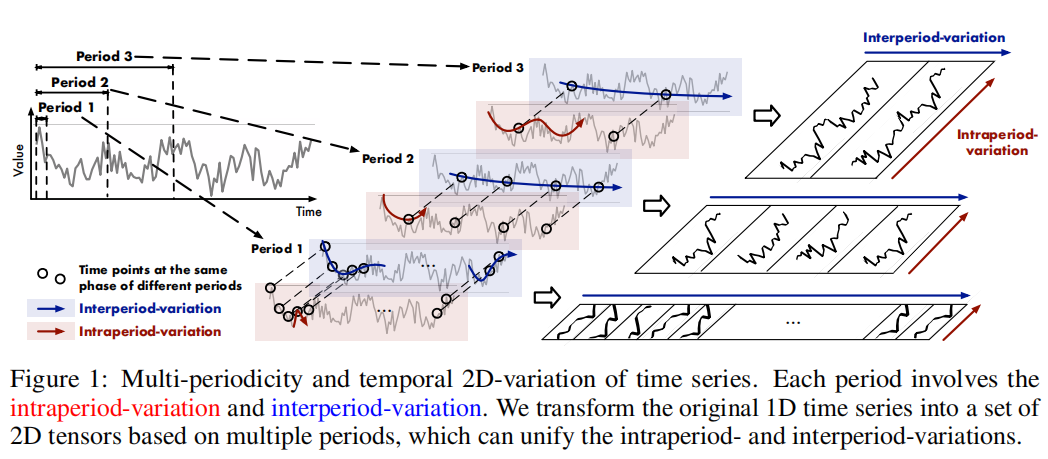
- 实际生活中的time series往往具有多周期性,比如天气观察每日/每年的波动,或者电力每周/每季的波动。这些多周期互相影响和覆盖,使时间变化的建模变得困难。
- 每个时间点的变化不仅受其周围点的影响,也受周围周期的影响。作者将其命名为周期内(intraperiod) 的变化和周期外(interperiod) 的变化,前者显示短期的时序模式,后者显示长期多个周期的时序变化趋势。
- 注意,如果一个时间序列无明显周期性,则作者将视它为一个无限长度的周期,通过周期内的变化来进行建模。
由于多周期性,作者提出了使用模块化的结构,通过单个模块来捕捉某个特定的周期中时序的变化,也可以将不同时间周期之间解耦。 但是1d时序模型比较难展示两种不同的变化,因此,作者将1d的问题延展到2d空间上。具体操作上是将1d时间序列转为2d tensor,每一列代表一个周期内的时间点,而每一行代表同意阶段的一些时间点在不同周期中的值。
作者通过流程得到了temporal 2d-variations(时序上的2d变化)
基于以上motivation,作者继续提出了TimesNet这样一个新的泛化时序分析模型,由多个TimesBlock组成,可以捕捉到多周期性、并获取模块化结构中对应的时序变化。
TimesBlock可以将1d时间序列转化为一组基于周期大小(可以通过学习)的2d tensors,再通过一个参数效率高的插入区块,捕捉周期内、周期外的时序变化。
主要算法
1d到2d转换
假设有一个长度为T的时间序列,有记录C个变量,原本的1d数据为 $\mathbf{X}_{1D}\in \mathbb{R}^{T \times C}$
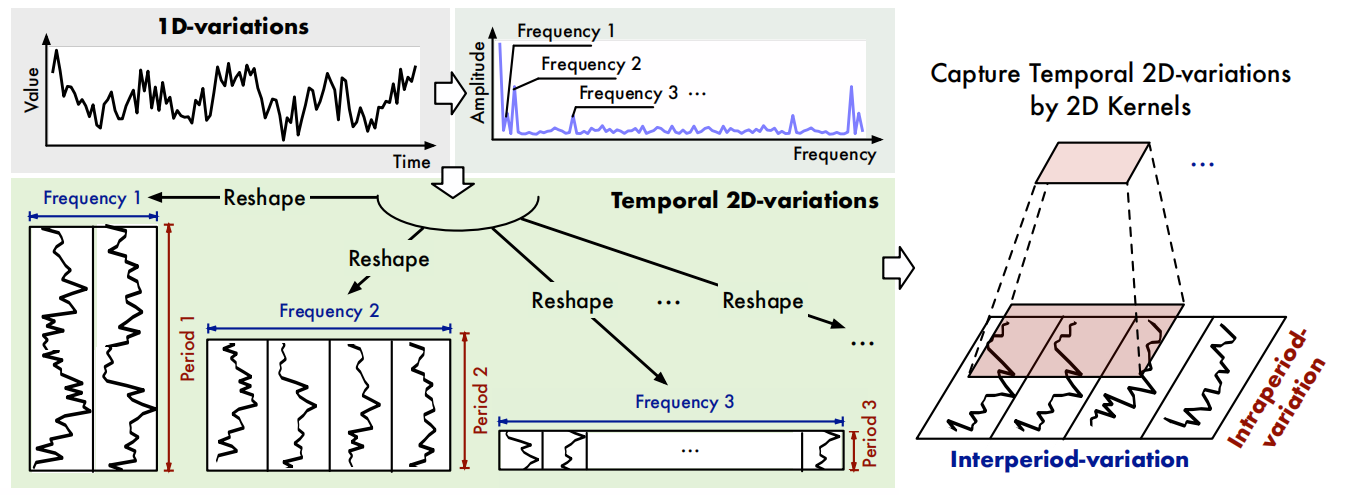
\[\mathbf{A}=\operatorname{Avg}\left(\operatorname{Amp}\left(\operatorname{FFT}\left(\mathbf{X}_{1 \mathrm{D}}\right)\right)\right),\left\{f_1, \cdots, f_k\right\}=\underset{f_* \in\left\{1, \cdots,\left[\frac{T}{2}\right]\right\}}{\arg \operatorname{Topk}}(\mathbf{A}), p_i=\left\lceil\frac{T}{f_i}\right\rceil, i \in\{1, \cdots, k\} \label{eq1}\tag{1}\]这里运用了FFT,将时间序列转换为频域信号,然后选择最显著的频率成分,以便更好地捕捉时间序列的周期性变化。FFT介绍可以看这篇:What is FFT?
由于频率信号的共轭性(FFT提取出的频率是在T/2处对称的),在频域信号中我们获得了 $f_1,…f_{T/2}$ 个频率,作者在这些频率中选择top-k个最显著,也就是振幅最大的频率 ${f_1,…f_k}$,k为一个超参数。
根据选择下来的top-k频率,计算出p_i=T/ f_k, 然后将1d信号按照p_i截取、reshape为2d,每列和每行分别代表周期内和周期间的变动。这样可以得到2d tensors ${X_{2D}^1, … X_{2D}^k}$, $\mathbf{X}_{2D}^i \in \mathbb{R}^{p_i\times f_i \times C}$
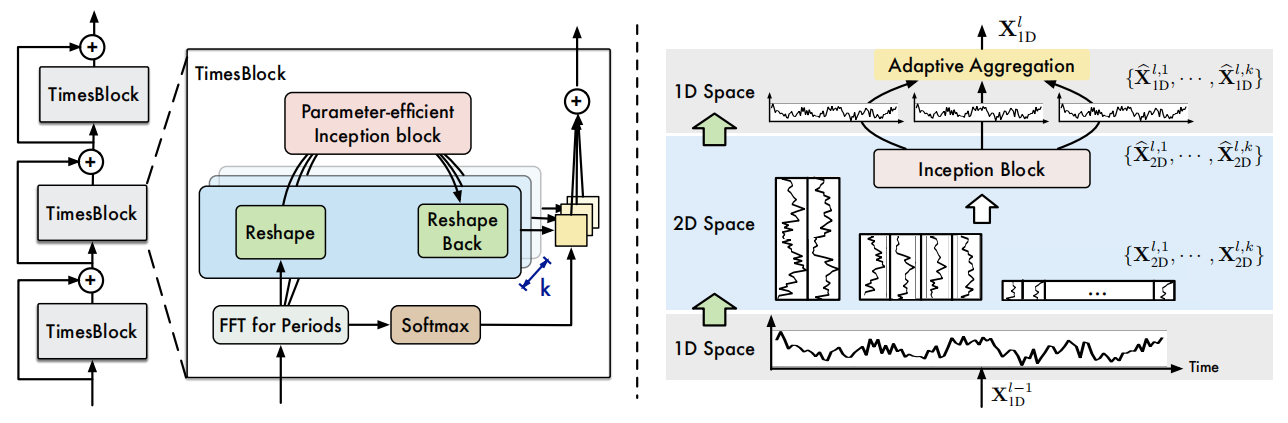
TimesBlock
更新公式: \(\mathbf{X}^l_{1D}=\operatorname{TimesBlock}(\mathbf{X}^{l-1}_{1D})+\mathbf{X}^{l-1}_{1D}\)
获取2d时序变化
可以根据公式(1)预测 $X_{1D}^{l-1}$ 的周期长度;然后通过周期长度将1d时间序列转为2d tensors。转换过后,使用Szedegy提出的parameter-efficient inception block,$\operatorname{Inception}(·)$,是经典的视觉骨干网络(根据代码这里使用的是 Inception Block V1 )。最后将2d时间序列展开,再使用阶段 $\operatorname{Trunc}(·)$ 去除之前填充 $\operatorname{Padding}(·)$ 过程中产生的0.
由于是从1D时间序列转换来的,2d核在inception block中可以将不同维度的cols和rows融合在一起(这里不太懂,可能要看代码)。另外,作者采用了共享的inception block给不同的2d tensors,使模型大小对超参数k选择无关。
Inception block Inception block是一种用于卷积神经网络(CNN)的模块化结构,旨在提高网络的表示能力和效率。它通过同时使用不同大小的卷积核和池化操作来捕获不同尺度的特征,从而使网络能够更好地适应不同尺度的特征。在本文中,作者使用参数高效的inception block来处理转换后的2D时间序列数据,以便更有效地捕捉多尺度的时间2D变化,并为后续的表示学习提供有益的信息
自适应融合 (Adaptive Aggregation)
最后,将k个1d信号融合在一起。由Auto Correlation启发,作者发现振幅A可以反映处选择频率的相对重要性。根据公式 $\eqref{eq1}$ 中获得的频率强度,经过Softmax函数变换为权重,对2d转换来的1d时序进行加权平均,作为下一个layer的输入。 \(\begin{aligned} \widehat{\mathbf{A}}_{f_1}^{l-1}, \cdots, \widehat{\mathbf{A}}_{f_k}^{l-1} & =\operatorname{Softmax}\left(\mathbf{A}_{f_1}^{l-1}, \cdots, \mathbf{A}_{f_k}^{l-1}\right) \\ \mathbf{X}_{1 \mathrm{D}}^l & =\sum_{i=1}^k \widehat{\mathbf{A}}_{f_i}^{l-1} \times \widehat{\mathbf{X}}_{1 \mathrm{D}}^{l, i} \end{aligned}\)
由于周期之间的时序波动已经被包括在结构化的2d tensor中,TimesBlock可以同时捕捉不同大小的2d时序变化。
2d视觉骨干网络的通用性
由于已经将信号转换为2d,作者声明可以使用计算机视觉领域的一些前沿模型来替代上面的Inception block来做表征学习,例如ResNet,ResNeXt,ConvNeXt,其他基于注意力机制的模型等。作者也测试了不同的表征模型,发现TimesNet可以通过使用性能更好的表征学习模型进行提升,比如ConvNeXt。
实验
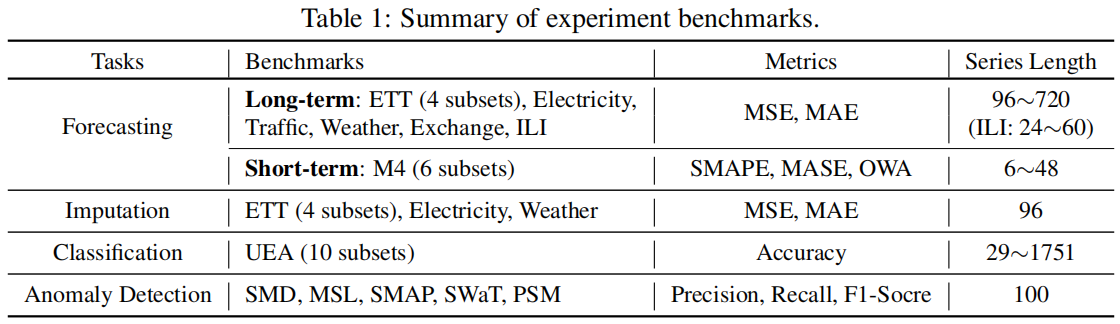
作者在时间序列的五大任务上分别进行实验:长期/短期的预测(Long/Short Term Forecasting)、缺失值填补(Imputation)、分类(Classification)、异常检测(Anomaly Detection)。这里异常检测使用的和anomaly transformer一样的数据集。
结果展示:
Appendix
Softmax
\[\operatorname{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{N}{e^{x_j}}}\]Softmax函数的主要作用是将一个含任意实数的向量转换成一个实数值在0到1之间的向量,并且转换后的所有值之和为1。向量中最大的数值对应的输出接近1,而其他数值对应的输出接近0,这使Softmax函数的输出非常适合用来表示概率分布。在神经网络和机器学习领域,Softmax函数主要用于多分类场景。
Representation Learning 表征学习
Representation Learning 是一种机器学习方法,它的目的是自动发现表示输入数据最好的方法,以便更容易完成分类、预测等任务。这种方法通常用在深度学习中,其中学习过程涉及识别或学习数据的有用特征,以用于识别或分类等任务。例如,在图像识别中,表示学习可能会学习识别边缘、角点、色块等特征。
这种学习方法与传统的机器学习方法不同,后者通常需要手动特征工程。表示学习自动寻找表示,从而降低了手动设计特征的需要。